Quantum Computing before Democritus
Imagine you are lost in a random labyrinth, looking for the exit. Or that you are the ancient Greek hero Theseus searching for the Minotaur in such a labyrinth.
How can we even describe a random labyrinth? Let us represent it by a network with n nodes, where each pair of nodes is connected only if you get heads after tossing a biased coin.
Imagine the Minotaur is standing in one of these nodes and has the power to determine how connected the labyrinth is, namely by controlling the bias of the coin whose tossing decides if each pair of nodes is connected or not.
Recently, it was proven that above a certain threshold of connectivity in the labyrinth (related to the bias of the coin), a quantum computer would offer the fastest way for Theseus to find the Minotaur [Physical Review Letters, 2016]. But below this threshold, that quantum speed-up would be lost, and Theseus would take longer to find his half-human enemy.
Is there something Theseus can do about it, or can the Minotaur always escape Theseus' quantum computational advantage by simply choosing the adequate bias for the coin?
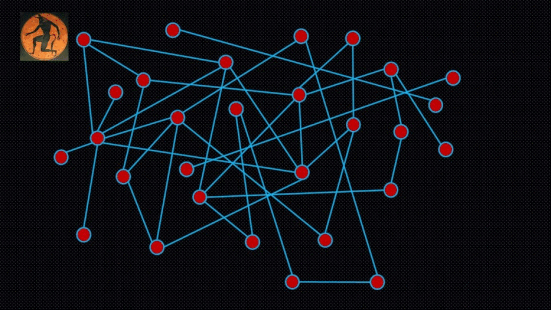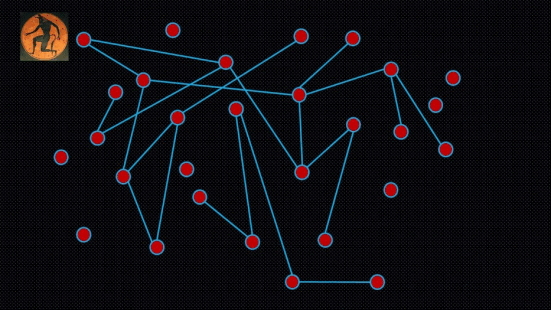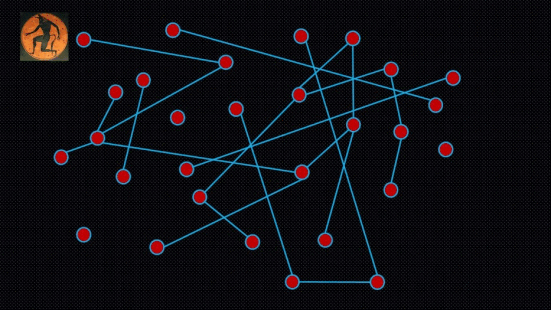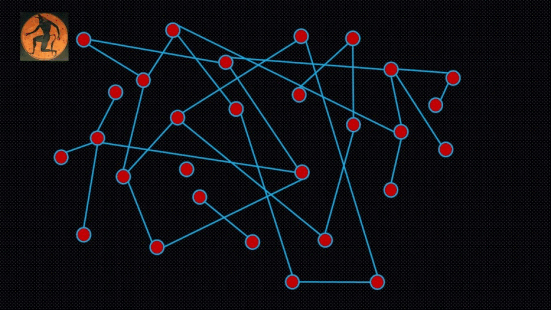
Imagine now that Theseus has the power to replace the entire labyrinth at regular time intervals. Each time, he deletes all the connections between the nodes, and then introduces new random connections by tossing the biased coin for each pair of nodes, thus effectively generating a new labyrinth. The number of nodes remains fixed. And the Minotaur is still the one deciding how connected or not the new random labyrinth is overall, by setting the bias of the coin. But Theseus can re-generate the labyrinth as frequently as he wants (see an example in the Figure below). That's his power.
In their work published in Physical Review Letters, Shantanav Chakraborty, Leonardo Novo, and Serena Di Giorgio, students from the Doctoral Programme in the Physics and Mathematics of Information at Instituto Superior Técnico (University of Lisbon), jointly with their supervisor Yasser Omar, all of them members of the Physics of Information and Quantum Technologies Group at Instituto de Telecomunicações, in Portugal, have proven that now the Minotaur can no longer escape the optimal quantum search by Theseus. In particular, whatever connectivity (or coin bias) the Minotaur chooses, there is always a frequency for generating new labyrinths that Theseus can choose to find the Minotaur in the fastest way possibly, taking full advantage of quantum computation. Even if the Minotaur imposes a bias leading to labyrinths with very low connectivity, including with many nodes isolated from the rest of the network, Theseus can simply generate new labyrinths more frequently and still use quantum search to find the Minotaur in the fastest way possible.
How can we even describe a random labyrinth? Let us represent it by a network with n nodes, where each pair of nodes is connected only if you get heads after tossing a biased coin.
Imagine the Minotaur is standing in one of these nodes and has the power to determine how connected the labyrinth is, namely by controlling the bias of the coin whose tossing decides if each pair of nodes is connected or not.
Recently, it was proven that above a certain threshold of connectivity in the labyrinth (related to the bias of the coin), a quantum computer would offer the fastest way for Theseus to find the Minotaur [Physical Review Letters, 2016]. But below this threshold, that quantum speed-up would be lost, and Theseus would take longer to find his half-human enemy.
Is there something Theseus can do about it, or can the Minotaur always escape Theseus' quantum computational advantage by simply choosing the adequate bias for the coin?
Imagine now that Theseus has the power to replace the entire labyrinth at regular time intervals. Each time, he deletes all the connections between the nodes, and then introduces new random connections by tossing the biased coin for each pair of nodes, thus effectively generating a new labyrinth. The number of nodes remains fixed. And the Minotaur is still the one deciding how connected or not the new random labyrinth is overall, by setting the bias of the coin. But Theseus can re-generate the labyrinth as frequently as he wants (see an example in the Figure below). That's his power.
In their work published in Physical Review Letters, Shantanav Chakraborty, Leonardo Novo, and Serena Di Giorgio, students from the Doctoral Programme in the Physics and Mathematics of Information at Instituto Superior Técnico (University of Lisbon), jointly with their supervisor Yasser Omar, all of them members of the Physics of Information and Quantum Technologies Group at Instituto de Telecomunicações, in Portugal, have proven that now the Minotaur can no longer escape the optimal quantum search by Theseus. In particular, whatever connectivity (or coin bias) the Minotaur chooses, there is always a frequency for generating new labyrinths that Theseus can choose to find the Minotaur in the fastest way possibly, taking full advantage of quantum computation. Even if the Minotaur imposes a bias leading to labyrinths with very low connectivity, including with many nodes isolated from the rest of the network, Theseus can simply generate new labyrinths more frequently and still use quantum search to find the Minotaur in the fastest way possible.
Figure: Can a quantum computer help Theseus find the Minotaur in the fastest way possible?
The authors found that the answer is yes, even when the random labyrinth is changing in time.
The authors found that the answer is yes, even when the random labyrinth is changing in time.
Besides an (altogether unexpected) taste for quantizing ancient Greek mythology, the motivation of the authors for their study was twofold: to investigate the robustness of analog quantum computation to time-varying defects, as well as to investigate the possibility of performing quantum information tasks on temporal networks.
Most real networks, be they social, natural or technological, like Facebook or the internet, are not static: they lose and gain links as time evolves. One would expect that when performing quantum computation in such messy, and more realistic, scenarios, the fragile quantum advantage would be lost. However, the authors found that this is not the case. They proved that the fundamental quantum search algorithm for finding a given node in a network retains its full quantum speed-up even for random networks varying in time. In fact, they show that one can use this temporal feature as a knob to control the performance of the computation. Furthermore, their results can also be exploited for networked quantum communication, well beyond the usual requirement where the sender and the receiver need a direct link to communicate quantumly. These discoveries open way to study quantum information technologies, for communication, computation and sensing, on realistic complex networks.
[ Note: The title of this popular summary is a reference to the book Quantum Computing since Democritus, by Scott Aaronson. ]
For more details, see the article:
S. Chakraborty, L. Novo, S. Di Giorgio, Y. Omar, Optimal quantum spatial search on random temporal networks, Physical Review Letters 119, 220503 (2017). Get PDF
S. Chakraborty, L. Novo, S. Di Giorgio, Y. Omar, Optimal quantum spatial search on random temporal networks, Physical Review Letters 119, 220503 (2017). Get PDF