An energy-efficient way of preparing a quantum system in a pure state
Most quantum information tasks rely on the ability to prepare a quantum system, with arbitrary accuracy, in a desired pure state. In a thermodynamic setting, this is brought about by transferring entropy from the system of interest to a thermal reservoir, resulting in a loss of energy – in the form of heat dissipation – to the reservoir.The minimal amount of heat dissipation incurred is proportional to the entropy reduction in the quantum system; this is referred to as Landauer’s limit. However, Landauer’s limit does not take into account the structure of the thermal reservoir itself – in most cases, the minimal achievable heat dissipation will actually be greater, and cannot be inferred from the entropy reduction alone.
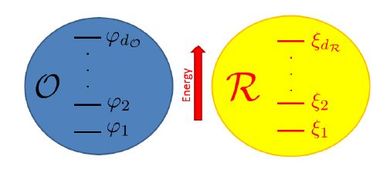
Schematic of the object we wish to prepare in a pure state O and the thermal reservoir we use for the process R.
The energy eigenstates of the reservoir are listed in increasing order of energy.
The energy eigenstates of the reservoir are listed in increasing order of energy.
In a recent paper titled Minimising the heat dissipation of quantum information erasure, written by M. H. Mohammady, M. Mohseni, and Y. Omar, this question has been addressed. By modelling the thermal reservoir as a quantum system that is initially at thermal equilibrium and is uncorrelated from the system of interest, and assuming that the composite system is thermally isolated,the authors propose a strategy to achieve the minimal achievable heat dissipation for any given accuracy of preparing the system in a pure state. This is accomplished by engineering the dynamics that the composite system undergoes. In situations where the energy structure of the reservoir is known, this work will allow scientists to assess how much the heat dissipation during the pure-state-preparation process can be reduced in principle.
For more details, see the article:
M. H. Mohammady, M. Mohseni, Y. Omar, Minimising the heat dissipation of quantum information erasure, New Journal of Physics 18, 015011
(2016). Get PDF